 |
EqWorld
The World of Mathematical Equations |
 |
Information >
Mathematical Books >
Handbook of Integral Equations, Second Edition > Contents
| |
 |
|
|
Handbook of Integral Equations
Second Edition, Updated, Revised and Extended
Publisher: Chapman & Hall/CRC Press
Publication Date: 14 February 2008
Number of Pages: 1144
|
Contents
- Authors
- Preface
- Some Remarks and Notation
Part I. Exact Solutions of Integral Equations
1. Linear Equations of the First Kind with Variable Limit of Integration
- 1.1. Equations Whose Kernels Contain Power-Law Functions
- 1.2. Equations Whose Kernels Contain Exponential Functions
- 1.3. Equations Whose Kernels Contain Hyperbolic Functions
- 1.4. Equations Whose Kernels Contain Logarithmic Functions
- 1.5. Equations Whose Kernels Contain Trigonometric Functions
- 1.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
- 1.7. Equations Whose Kernels Contain Combinations of Elementary Functions
- 1.8. Equations Whose Kernels Contain Special Functions
- 1.9. Equations Whose Kernels Contain Arbitrary Functions
- 1.10. Some Formulas and Transformations
2. Linear Equations of the Second Kind with Variable Limit of Integration
- 2.1. Equations Whose Kernels Contain Power-Law Functions
- 2.2. Equations Whose Kernels Contain Exponential Functions
- 2.3. Equations Whose Kernels Contain Hyperbolic Functions
- 2.4. Equations Whose Kernels Contain Logarithmic Functions
- 2.5. Equations Whose Kernels Contain Trigonometric Functions
- 2.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
- 2.7. Equations Whose Kernels Contain Combinations of Elementary Functions
- 2.8. Equations Whose Kernels Contain Special Functions
- 2.9. Equations Whose Kernels Contain Arbitrary Functions
- 2.10. Some Formulas and Transformations
3. Linear Equations of the First Kind with Constant Limits of Integration
- 3.1. Equations Whose Kernels Contain Power-Law Functions
- 3.2. Equations Whose Kernels Contain Exponential Functions
- 3.3. Equations Whose Kernels Contain Hyperbolic Functions
- 3.4. Equations Whose Kernels Contain Logarithmic Functions
- 3.5. Equations Whose Kernels Contain Trigonometric Functions
- 3.6. Equations Whose Kernels Contain Combinations of Elementary Functions
- 3.7. Equations Whose Kernels Contain Special Functions
- 3.8. Equations Whose Kernels Contain Arbitrary Functions
- 3.9. Dual Integral Equations of the First Kind
4. Linear Equations of the Second Kind with Constant Limits of Integration
- 4.1. Equations Whose Kernels Contain Power-Law Functions
- 4.2. Equations Whose Kernels Contain Exponential Functions
- 4.3. Equations Whose Kernels Contain Hyperbolic Functions
- 4.4. Equations Whose Kernels Contain Logarithmic Functions
- 4.5. Equations Whose Kernels Contain Trigonometric Functions
- 4.6. Equations Whose Kernels Contain Inverse Trigonometric Functions
- 4.7. Equations Whose Kernels Contain Combinations of Elementary Functions
- 4.8. Equations Whose Kernels Contain Special Functions
- 4.9. Equations Whose Kernels Contain Arbitrary Functions
- 4.10. Some Formulas and Transformations
5. Nonlinear Equations of the First Kind with Variable Limit of Integration
- 5.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
- 5.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
- 5.3. Equations with Nonlinearity of General Form
6. Nonlinear Equations of the Second Kind with Variable Limit of Integration
- 6.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
- 6.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
- 6.3. Equations with Power-Law Nonlinearity
- 6.4. Equations with Exponential Nonlinearity
- 6.5. Equations with Hyperbolic Nonlinearity
- 6.6. Equations with Logarithmic Nonlinearity
- 6.7. Equations with Trigonometric Nonlinearity
- 6.8. Equations with Nonlinearity of General Form
7. Nonlinear Equations of the First Kind with Constant Limits of Integration
- 7.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
- 7.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
- 7.3. Equations with Power-Law Nonlinearity That Contain Arbitrary Functions
- 7.4. Equations with Nonlinearity of General Form
8. Nonlinear Equations of the Second Kind with Constant Limits of Integration
- 8.1. Equations with Quadratic Nonlinearity That Contain Arbitrary Parameters
- 8.2. Equations with Quadratic Nonlinearity That Contain Arbitrary Functions
- 8.3. Equations with Power-Law Nonlinearity
- 8.4. Equations with Exponential Nonlinearity
- 8.5. Equations with Hyperbolic Nonlinearity
- 8.6. Equations with Logarithmic Nonlinearity
- 8.7. Equations with Trigonometric Nonlinearity
- 8.8. Equations with Nonlinearity of General Form
Part II. Methods for Solving Integral Equations
9. Main Definitions and Formulas. Integral Transforms
- 9.1. Some Definitions, Remarks, and Formulas
- 9.2. Laplace Transform
- 9.3. Mellin Transform
- 9.4. Fourier Transform
- 9.5. Fourier Cosine and Sine Transforms
- 9.6. Other Integral Transforms
10. Methods for Solving Linear Equations of the Form
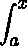 K(x,t) y(t) dt = f(x) K(x,t) y(t) dt = f(x)
- 10.1. Volterra Equations of the First Kind
- 10.2. Equations with Degenerate Kernel: K(x,t) = g1(x)h1(t) + ... + gn(x)hn(t)
- 10.3. Reduction of Volterra Equations of the First Kind to Volterra Equations of the Second Kind
- 10.4. Equations with Difference Kernel: K(x,t) = K(x − t)
- 10.5. Method of Fractional Differentiation
- 10.6. Equations with Weakly Singular Kernel
- 10.7. Method of Quadratures
- 10.8. Equations with Infinite Integration Limit
11. Methods for Solving Linear Equations of the Form
y(x) − 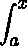 K(x,t) y(t) dt = f(x) K(x,t) y(t) dt = f(x)
- 11.1. Volterra Integral Equations of the Second Kind
- 11.2. Equations with Degenerate Kernel: K(x,t) = g1(x)h1(t) + ... + gn(x)hn(t)
- 11.3. Equations with Difference Kernel: K(x,t) = K(x − t)
- 11.4. Operator Methods for Solving Linear Integral Equations
- 11.5. Construction of Solutions of Integral Equations with Special Right-Hand Side
- 11.6. Method of Model Solutions
- 11.7. Method of Differentiation for Integral Equations
- 11.8. Reduction of Volterra Equations of the Second Kind to Volterra Equations of the First Kind
- 11.9. Successive Approximation Method
- 11.10. Method of Quadratures
- 11.11. Equations with Infinite Integration Limit
12. Methods for Solving Linear Equations of the Form
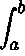 K(x,t) y(t) dt = f(x) K(x,t) y(t) dt = f(x)
- 12.1. Some Definition and Remarks
- 12.2. Integral Equations of the First Kind with Symmetric Kernel
- 12.3. Integral Equations of the First Kind with Nonsymmetric Kernel
- 12.4. Method of Differentiation for Integral Equations
- 12.5. Method of Integral Transforms
- 12.6. Krein's Method and Some Other Exact Methods for Integral Equations of Special Types
- 12.7. Riemann Problem for the Real Axis
- 12.8. Carleman Method for Equations of the Convolution Type of the First Kind
- 12.9. Dual Integral Equations of the First Kind
- 12.10. Asymptotic Methods for Solving Equations with Logarithmic Singularity
- 12.11. Regularization Methods
- 12.12. Fredholm Integral Equation of the First Kind as an Ill-Posed Problem
13. Methods for Solving Linear Equations of the Form
y(x) − 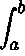 K(x,t) y(t) dt = f(x) K(x,t) y(t) dt = f(x)
- 13.1. Some Definition and Remarks
- 13.2. Fredholm Equations of the Second Kind with Degenerate Kernel. Some Generalizations
- 13.3. Solution as a Power Series in the Parameter. Method of Successive Approximations
- 13.4. Method of Fredholm Determinants
- 13.5. Fredholm Theorems and the Fredholm Alternative
- 13.6. Fredholm Integral Equations of the Second Kind with Symmetric Kernel
- 13.7. Integral Equations with Nonnegative Kernels
- 13.8. Operator Method for Solving Integral Equations of the Second Kind
- 13.9. Methods of Integral Transforms and Model Solutions
- 13.10. Carleman Method for Integral Equations of Convolution Type of the Second Kind
- 13.11. Wiener–Hopf Method
- 13.12. Krein's Method for Wiener–Hopf Equations
- 13.13. Methods for Solving Equations with Difference Kernels on a Finite Interval
- 13.14. Method of Approximating a Kernel by a Degenerate One
- 13.15. Bateman Method
- 13.16. Collocation Method
- 13.17. Method of Least Squares
- 13.18. Bubnov–Galerkin Method
- 13.19. Quadrature Method
- 13.20. Systems of Fredholm Integral Equations of the Second Kind
- 13.21. Regularization Method for Equations with Infinite Limits of Integration
14. Methods for Solving Singular Integral Equations of the First Kind
- 14.1. Some Definitions and Remarks
- 14.2. Cauchy Type Integral
- 14.3. Riemann Boundary Value Problem
- 14.4. Singular Integral Equations of the First Kind
- 14.5. Multhopp–Kalandiya Method
- 14.6. Hypersingular Integral Equations
15. Methods for Solving Complete Singular Integral Equations
- 15.1. Some Definitions and Remarks
- 15.2. Carleman Method for Characteristic Equations
- 15.3. Complete Singular Integral Equations Solvable in a Closed Form
- 15.4. Regularization Method for Complete Singular Integral Equations
- 15.5. Analysis of Solutions Singularities for Complete Integral Equations with Generalized Cauchy Kernels
- 15.6. Direct Numerical Solution of Singular Integral Equations with Generalized Kernels
16. Methods for Solving Nonlinear Integral Equations
- 16.1. Some Definitions and Remarks
- 16.2. Exact Methods for Nonlinear Equations with Variable Limit of Integration
- 16.3. Approximate and Numerical Methods for Nonlinear Equations with Variable Limit of Integration
- 16.4. Exact Methods for Nonlinear Equations with Constant Integration Limits
- 16.5. Approximate and Numerical Methods for Nonlinear Equations with Constant Integration Limits
- 16.6. Existence and Uniqueness Theorems for Nonlinear Equations
- 16.7. Nonlinear Equations with a Parameter: Eigenfunctions, Eigenvalues, Bifurcation Points
17. Methods for Solving Multidimensional Mixed Integral Equations
- 17.1. Some Definition and Remarks
- 17.2. Methods of Solution of Mixed Integral Equations on a Finite Interval
- 17.3. Methods of Solving Mixed Integral Equations on a Ring-Shaped Domain
- 17.4. Projection Method for Solving Mixed Equations on a Bounded Set
18. Application of Integral Equations for the Investigation of Differential Equations
- 18.1. Reduction of the Cauchy Problem for ODEs to Integral Equations
- 18.2. Reduction of Boundary Value Problems for ODEs to Volterra Integral Equations. Calculation of Eigenvalues
- 18.3. Reduction of Boundary Value Problems for ODEs to Fredholm Integral Equations with the Help of the Green's Function
- 18.4. Reduction of PDEs with Boundary Conditions of the Third Kind to Integral Equations
- 18.5. Representation of Linear Boundary Value Problems in Terms of Potentials
- 18.6. Representation of Solutions of Nonlinear PDEs in Terms of Solutions of Linear Integral Equations (Inverse Scattering)
Supplements
Supplement 1. Elementary Functions and Their Properties
- 1.1. Power, Exponential, and Logarithmic Functions
- 1.2. Trigonometric Functions
- 1.3. Inverse Trigonometric Functions
- 1.4. Hyperbolic Functions
- 1.5. Inverse Hyperbolic Functions
Supplement 2. Finite Sums and Infinite Series
- 2.1. Finite Numerical Sums
- 2.2. Finite Functional Sums
- 2.3. Infinite Numerical Series
- 2.4. Infinite Functional Series
Supplement 3. Tables of Indefinite Integrals
- 3.1. Integrals Involving Rational Functions
- 3.2. Integrals Involving Irrational Functions
- 3.3. Integrals Involving Exponential Functions
- 3.4. Integrals Involving Hyperbolic Functions
- 3.5. Integrals Involving Logarithmic Functions
- 3.6. Integrals Involving Trigonometric Functions
- 3.7. Integrals Involving Inverse Trigonometric Functions
Supplement 4. Tables of Definite Integrals
- 4.1. Integrals Involving Power-Law Functions
- 4.2. Integrals Involving Exponential Functions
- 4.3. Integrals Involving Hyperbolic Functions
- 4.4. Integrals Involving Logarithmic Functions
- 4.5. Integrals Involving Trigonometric Functions
- 4.6. Integrals Involving Bessel Functions
Supplement 5. Tables of Laplace Transforms
- 5.1. General Formulas
- 5.2. Expressions with Power-Law Functions
- 5.3. Expressions with Exponential Functions
- 5.4. Expressions with Hyperbolic Functions
- 5.5. Expressions with Logarithmic Functions
- 5.6. Expressions with Trigonometric Functions
- 5.7. Expressions with Special Functions
Supplement 6. Tables of Inverse Laplace Transforms
- 6.1. General Formulas
- 6.2. Expressions with Rational Functions
- 6.3. Expressions with Square Roots
- 6.4. Expressions with Arbitrary Powers
- 6.5. Expressions with Exponential Functions
- 6.6. Expressions with Hyperbolic Functions
- 6.7. Expressions with Logarithmic Functions
- 6.8. Expressions with Trigonometric Functions
- 6.9. Expressions with Special Functions
Supplement 7. Tables of Fourier Cosine Transforms
- 7.1. General Formulas
- 7.2. Expressions with Power-Law Functions
- 7.3. Expressions with Exponential Functions
- 7.4. Expressions with Hyperbolic Functions
- 7.5. Expressions with Logarithmic Functions
- 7.6. Expressions with Trigonometric Functions
- 7.7. Expressions with Special Functions
Supplement 8. Tables of Fourier Sine Transforms
- 8.1. General Formulas
- 8.2. Expressions with Power-Law Functions
- 8.3. Expressions with Exponential Functions
- 8.4. Expressions with Hyperbolic Functions
- 8.5. Expressions with Logarithmic Functions
- 8.6. Expressions with Trigonometric Functions
- 8.7. Expressions with Special Functions
Supplement 9. Tables of Mellin Transforms
- 9.1. General Formulas
- 9.2. Expressions with Power-Law Functions
- 9.3. Expressions with Exponential Functions
- 9.4. Expressions with Logarithmic Functions
- 9.5. Expressions with Trigonometric Functions
- 9.6. Expressions with Special Functions
Supplement 10. Tables of Inverse Mellin Transforms
- 10.1. Expressions with Power-Law Functions
- 10.2. Expressions with Exponential and Logarithmic Functions
- 10.3. Expressions with Trigonometric Functions
- 10.4. Expressions with Special Functions
Supplement 11. Special Functions and Their Properties
- 11.1. Some Coefficients, Symbols, and Numbers
- 11.2. Error Functions. Exponential and Logarithmic Integrals
- 11.3. Sine Integral and Cosine Integral. Fresnel Integrals
- 11.4. Gamma Function, Psi Function, and Beta Function
- 11.5. Incomplete Gamma and Beta Functions
- 11.6. Bessel Functions (Cylindrical Functions)
- 11.7. Modified Bessel Functions
- 11.8. Airy Functions
- 11.9. Confluent Hypergeometric Functions
- 11.10. Gauss Hypergeometric Functions
- 11.11. Legendre Polynomials, Legendre Functions, and Associated Legendre Functions
- 11.12. Parabolic Cylinder Functions
- 11.13. Elliptic Integrals
- 11.14. Elliptic Functions
- 11.15. Jacobi Theta Functions
- 11.16. Mathieu Functions and Modified Mathieu Functions
- 11.17. Orthogonal Polynomials
- 11.18. Nonorthogonal Polynomials
Supplement 12. Some Notions of Functional Analysis
- 12.1. Functions of Bounded Variation
- 12.2. Stieltjes Integral
- 12.3. Lebesgue Integral
- 12.4. Linear Normed Spaces
- 12.5. Euclidean and Hilbert Spaces. Linear Operators in Hilbert Spaces
References
Index
|
The EqWorld website presents extensive information on solutions to
various classes of ordinary differential equations, partial differential
equations, integral equations, functional equations, and other mathematical
equations.
Copyright © 2008 Andrei D. Polyanin
|



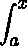 K(x,t) y(t) dt = f(x)
K(x,t) y(t) dt = f(x)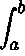 K(x,t) y(t) dt = f(x)
K(x,t) y(t) dt = f(x)