 |
EqWorld Мир математических уравнений |
 |
Точные решения > Интегральные уравнения> Интегральные уравнения Фредгольма второго рода и родственные линейные уравнения с постоянными пределами интегрирования
4. Интегральные уравнения Фредгольма второго рода
4-1. Интегральные уравнения, ядра которых содержат степенные функции
-
y(x) − λ
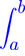 (x − t)y(t) dt = f(x).
(x − t)y(t) dt = f(x).
-
y(x) + A
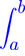 |x − t|y(t) dt = f(x).
|x − t|y(t) dt = f(x).
-
Ay(x) + Bπ−1
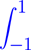 (t − x)−1y(t) dt = f(x).
(t − x)−1y(t) dt = f(x).
-
y(x) − λ
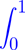 [(t − x)−1 − (x + t − 2xt)−1]
y(t) dt = f(x).
Уравнение Трикоми.
[(t − x)−1 − (x + t − 2xt)−1]
y(t) dt = f(x).
Уравнение Трикоми.
4-2. Интегральные уравнения, ядра которых содержат экспоненциальные или гиперболические функции
-
y(x) + λ
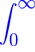 e − |x − t|y(t) dt = f(x).
e − |x − t|y(t) dt = f(x).
-
y(x) − λ
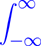 e − |x − t|y(t) dt = 0.
Лалеско--Пикара.
e − |x − t|y(t) dt = 0.
Лалеско--Пикара.
-
y(x) + λ
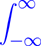 e − |x − t|y(t) dt = f(x).
e − |x − t|y(t) dt = f(x).
-
y(x) + A
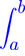 eλ|x − t|y(t) dt = f(x).
eλ|x − t|y(t) dt = f(x).
-
y(x) + λ
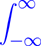 {cosh[b(x − t)]}−1y(t) dt = f(x).
{cosh[b(x − t)]}−1y(t) dt = f(x).
4-3. Интегральные уравнения, ядра которых содержат тригонометрические функции
-
y(x) − λ
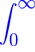 cos(xt)y(t) dt = f(x).
cos(xt)y(t) dt = f(x).
-
y(x) − λ
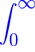 sin(xt)y(t) dt = f(x).
sin(xt)y(t) dt = f(x).
-
y(x) − λ
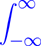 sin(x − t)(x − t)−1y(t) dt
= f(x).
sin(x − t)(x − t)−1y(t) dt
= f(x).
-
Ay(x) − B(2π)−1
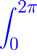 cot(t/2 − x/2)y(t) dt = f(x).
cot(t/2 − x/2)y(t) dt = f(x).
-
y(x) − λ
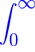 eμ(x − t) cos(xt)y(t) dt = f(x).
eμ(x − t) cos(xt)y(t) dt = f(x).
-
y(x) − λ
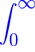 eμ(x − t) sin(xt)y(t) dt = f(x).
eμ(x − t) sin(xt)y(t) dt = f(x).
4-4. Интегральные уравнения, ядра которых содержат произвольные функции
-
y(x) −
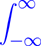 K(x − t)y(t) dt = f(x).
K(x − t)y(t) dt = f(x).
-
y(x) −
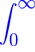 K(x − t)y(t) dt = f(x).
Уравнение Винера--Хопфа второго рода.
K(x − t)y(t) dt = f(x).
Уравнение Винера--Хопфа второго рода.
Веб-сайт EqWorld содержит обширную информацию о решениях различных классов обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, интегральных уравнений, функциональных уравнений и других математических уравнений.
Copyright © 2004-2017 А. Д. Полянин