EqWorld logo

EqWorld

The World of Mathematical Equations

 IPM Logo

Exact Solutions Methods Software For Authors Math Forums

Exact Solutions > Interesting Papers > N.A. Kudryashov. Seven common errors in finding exact solutions of nonlinear differential equations > 4. Third error...

Seven common errors in finding exact solutions of nonlinear differential equations
© N.A. Kudryashov
Communications in Nonlinear Science and Numerical Simulation (to be pubslished in 2009)

Contents

  1. Abstract
  2. Introduction
  3. First error: some authors use equivalent methods to find exact solutions
  4. Second error: some authors do not use the known general solutions of ordinary differential equations
  5. Third error: some authors omit arbitrary constants after integration of equation
  6. Fourth error: using some functions in finding exact solutions some authors lose arbitrary constants
  7. Fifth error: some authors do not simplify the solutions of differential equations
  8. Sixth error: some authors do not check solutions of differential equations
  9. Seventh error: some authors include additional arbitrary constants into solutions
  10. Conclusion
  11. References

4. Third error: some authors omit arbitrary constants after integration of equation

Reductions of nonlinear evolution equations to nonlinear ordinary differential equations can be often integrated. However, some authors assume, that the arbitrary constants of integration are equal to zero. This error potentially leads to the loss of the arbitrary constants in the final expression. So the solution obtained in such way is less general than it could be. The third common error can be formulated as follows.

Third error. Some authors omit the arbitrary constants after integrating of the nonlinear ordinary differential equations.

Example 3a. Reduction of the Burgers equation by Soliman [51].

Soliman  [51] considered the Burgers equation
ut + u ux - ν uxx = 0
(4.1)

to solve this equation by so called ”the modified extended tanh - function method”.

It is well known, that by using the Cole-Hopf transformation  [52, 53]
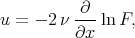∂ u = - 2 ν---lnF, ∂x
(4.2)

we can write the equality
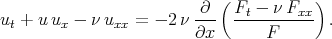( ) ut + uux - ν uxx = - 2ν -∂- Ft---ν-Fxx . ∂x F
(4.3)

From the last relation we can see, that each solution of the heat equation
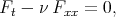Ft - ν Fxx = 0,
(4.4)

gives the solution of the Burgers equation by formula (4.2).

However to find the solutions of the Burgers equation Soliman  [51] used the travelling wave solutions 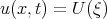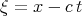u(x,t) = U (ξ ), ξ = x - ct and from Eq.(4.1) after integration with respect to 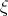ξ the author obtained the equation in the form
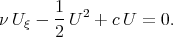1 ν U ξ ---U2 + cU = 0. 2
(4.5)

The constant of integration he took to be equal to zero. The general solution of Eq.(4.5) takes the form
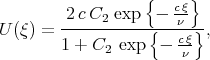{ } 2c C exp - cξ U(ξ) = -----2-----{---ν-}, 1 + C2 exp - cνξ
(4.6)

where C2 is an arbitrary constant.

The general solution of Eq.(4.5) has the only arbitrary constant. But if we take nonzero constant of integration in Eq.(4.5), we can have two arbitrary constants in the solution.

Example 3b. Reduction of the (2+1) - dimensional Konopelchenko - Dubrovsky equation by Abdou [54]
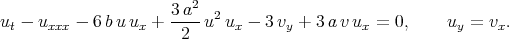2 u - u - 6 bu u + 3-a-u2 u - 3v + 3 av u = 0, u = v . t xxx x 2 x y x y x
(4.7)
Using the wave solutions
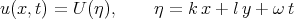u(x, t) = U (η), η = kx + ly + ω t
(4.8)
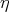the author  [54] looked for the exact solutions of Eq.(4.7). After integration with respect to η he obtained the second order differential equation
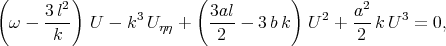( 2) ( ) 2 ω - 3-l- U - k3U + 3al-- 3 bk U 2 + a--kU 3 = 0, k ηη 2 2
(4.9)
but the zero constant of integration was taken. Abdou  [54] used the Exp - function method to look for solitary wave solutions of Eq.(4.9).

However multiplying Eq.(4.9) on 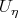U η and integrating this equation with respect to η again, we have the equation
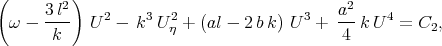( 2) 2 ω - 3l-- U 2 - k3 Uη2+ (al - 2b k) U3 + a-k U 4 = C2, k 4
(4.10)
where C2 is a constant of integration. The general solution of Eq.(4.10) is expressed via the Jacobi elliptic function  [7].

Example 3c. Reduction of the Ito equation by Wazwaz  [55]
v + v + 6 v v + 3v v + 3v v = 0. xtt xxxxt xx xt x xxt xxx t
(4.11)

The author  [55] looked for the solutions of Eq. (4.11) taking into account the travelling wave
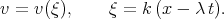v = v(ξ), ξ = k (x - λt).
(4.12)

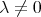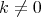Substituting (4.12) into (4.11) Wazwaz obtained when λ ⁄= 0 and k ⁄= 0 the equation in the form
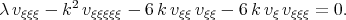λv - k2v - 6 kv v - 6k v v = 0. ξξξ ξξξξξ ξξ ξξ ξ ξξξ
(4.13)

Integrating Eq.(4.13) twice with respect to 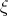ξ one can have the equation
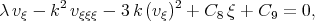λv ξ - k2 vξξξ - 3k (vξ)2 + C8 ξ + C9 = 0,
(4.14)
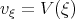where C8 and C9 are arbitrary constants. Denoting vξ = V (ξ ) in Eq. (4.14) we get the equation
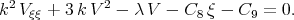2 2 k Vξξ + 3 kV - λ V - C8 ξ - C9 = 0.
(4.15)

The general solution of this equation was discussed above in example 2b.

However the author  [55] looked for solutions of Eq. (4.14) for C8 = 0 and C9 = 0 taking into consideration the tanh - coth method and did not present the general solution of Eq. (4.13).

Example 3d. Reduction of the Boussinesq equation by Bekir  [32]
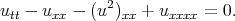u - u - (u2) + u = 0. tt xx xx xxxx
(4.16)
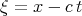Using the wave variable ξ = x - ct the author  [32] got the equation
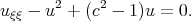u ξξ - u2 + (c2 - 1)u = 0.
(4.17)
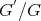To look for the solitary wave solutions of Eq.(4.17) the author  [32] used the G ′∕G - method, but he have been omitted two arbitrary constants after the integration.

In fact, from Eq.(4.16) we obtain the second order differential equation in the form
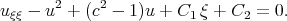2 2 u ξξ - u + (c - 1)u + C1 ξ + C2 = 0.
(4.18)
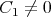The general solution of Eq.(4.18) is expressed at C1 ⁄= 0 via the first Painlevé transcendents. In the case C1 = 0 solutions of Eq.(4.18) is determined by the Weierstrass elliptic function. All possible solutions of Eq. (4.16) were obtained in work  [56].

The EqWorld website presents extensive information on solutions to various classes of ordinary differential equations, partial differential equations, integral equations, functional equations, and other mathematical equations.

Copyright © 2004-2017 Andrei D. Polyanin