EqWorld logo

EqWorld

The World of Mathematical Equations

 IPM Logo

Exact Solutions Methods Software For Authors Math Forums

Exact Solutions > Interesting Papers > N.A. Kudryashov. Seven common errors in finding exact solutions of nonlinear differential equations > 6. Fifth error...

Seven common errors in finding exact solutions of nonlinear differential equations
© N.A. Kudryashov
Communications in Nonlinear Science and Numerical Simulation (to be pubslished in 2009)

Contents

  1. Abstract
  2. Introduction
  3. First error: some authors use equivalent methods to find exact solutions
  4. Second error: some authors do not use the known general solutions of ordinary differential equations
  5. Third error: some authors omit arbitrary constants after integration of equation
  6. Fourth error: using some functions in finding exact solutions some authors lose arbitrary constants
  7. Fifth error: some authors do not simplify the solutions of differential equations
  8. Sixth error: some authors do not check solutions of differential equations
  9. Seventh error: some authors include additional arbitrary constants into solutions
  10. Conclusion
  11. References

6. Fifth error: some authors do not simplify the solutions of differential equations

Using different approaches for nonlinear differential equations, the authors obtain different forms of the solutions and sometimes they find the solutions in cumbersome forms. Interpretation and understanding of such solutions are difficult and we believe, that these solutions can be simplified. The consequence of the cumbersome expressions is a risk of misprints. The solutions in cumbersome form give an illusion that the authors indeed find new solutions. We meet many such solutions of nonlinear differential equations especially found by means of the Exp — function method. Another consequence is the fact, that the authors obtain the same solutions expressed in different forms, because it is well known, that trigonometric and hyperbolic expressions admit different representation.

The fifth error can be formulated as follows.

Fifth error. Expressions for solutions of nonlinear differential equations are often not simplified.

Example 5a. Solutions of the Jimbo - Miva equation (3.26) by Öziş and Aslan  [48].

Using the Exp - function method Öziş and Aslan  [48] found some solitary wave solutions of Eq. (3.26), but a number of these solutions can be simplified. For example solution (30) in  [48] is transformed by the following set of equalities
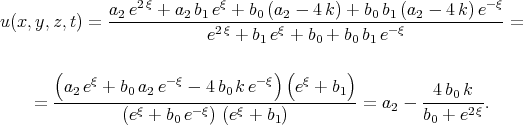a2e2ξ + a2b1 eξ + b0(a2 - 4 k) + b0b1(a2 - 4k )e-ξ u(x,y, z,t) = -------------2ξ------ξ--------------ξ-------------= e + b1e + b0 + b0b1 e ( ) ( ) a eξ + b a e-ξ - 4b k e-ξ eξ + b = --2------0-2---------0--------------1-= a2 - -4-b0k--. (eξ + b0e-ξ) (eξ + b1) b0 + e2ξ
(6.1)

It is seen, that the last expression is better for understanding, then the solution by Öziş and Aslan.

Example 5b. Solutions of the Konopelchenko - Dubrovsky equation (4.7) by Abdou  [54].

By means of the Exp - function method Abdou  [54] obtained some solitary wave solutions of Eq. (4.7), but some solutions can be simplified. For example solution (42) in  [54] reduces to
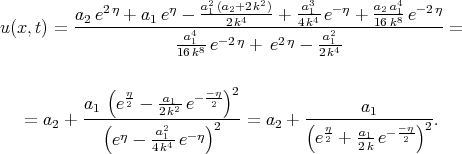a2(a +2k2) a3 a a4 a2-e2η +-a1-eη --1-22k4----+-41k4 e--η +-216-1k8-e-2η u(x,t) = -a41- -2η 2η a21- = 16k8 e + e - 2k4 ( η a - -η)2 a1--e-2 --21k2 e-2--- -------a1------- = a2 + ( a2 )2 = a2 + ( η a1 - -η)2. eη - 41k4 e-η e 2 + 2k e 2
(6.2)

Example 5c. Solution of the modified Benjamin - Bona - Mahony equation by Yusufoǧlu [63]
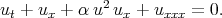u + u + α u2 u + u = 0. t x x xxx
(6.3)

Using the travelling wave the author  [63] obtained the equation
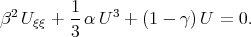2 1- 3 β U ξξ + 3 α U + (1 - γ )U = 0.
(6.4)

Yusufoǧlu  [63] found the solution of Eq.(6.4) in the form
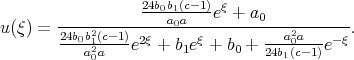24b0ba1(ac--1)eξ + a0 u (ξ) = 24b0b2(c-1)-----0-------------a2a-----. ---a120a---e2ξ + b1eξ + b0 + 24b10(c-1)e-ξ
(6.5)

Solution (6.5) has three arbitrary constants a0, b0 and b1, but in fact this solution can be simplified using the set of equalities
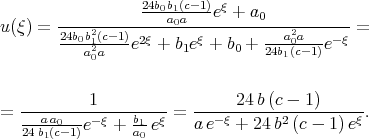24b0b1(c--1)eξ + a0 u(ξ) = 24bb2(c-1)-----a0a------------a2a------= --0a12a---e2ξ + b1eξ + b0 + 24b10(c--1)e-ξ 0 ---------1--------- -----24-b(c --1)------ = ---aa0--e-ξ + b1e ξ = ae- ξ + 24 b2(c - 1)eξ. 24b1(c-1) a0
(6.6)

We can see, that solution (6.6) contains the only arbitrary constant 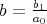b = b1 a0.

Note that Eq.(6.3) can be easy transformed to the modified KdV equation and this equation is not the BBM equation.

Example 5d. Solutions of the fifth - order KdV equation by Chun  [64]
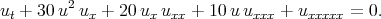ut + 30 u2ux + 20ux uxx + 10u uxxx + uxxxxx = 0.
(6.7)

Using the Exp - function method, Chun obtained seventeen exact solutions of Eq. (6.7)  [64]. His first solution (formula (25) in  [64]) can be simplified to the trivial solution, because
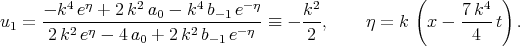4 η 2 4 -η 2 ( 4 ) u1 = - k-e-+--2k--a0 --k-b-1e----≡ - k-, η = k x - 7k--t . 2 k2eη - 4a0 + 2 k2b- 1e-η 2 4
(6.8)

The sixth solution by Chun (formula (30)  [64]) can be simplified to the trivial solution as well
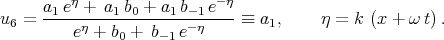a1-eη +-a1b0-+-a1b--1e-η u6 = eη + b0 + b-1e- η ≡ a1, η = k (x + ω t).
(6.9)

The thirteenth (as well as the fourteenth and the fifteenth) solution (formula (69) in paper  [64]) is also constant as we can see from the equality
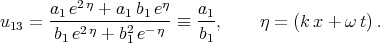a1-e2η +-a1-b1eη a1- u13 = b1e2η + b21e- η ≡ b1, η = (k x + ω t).
(6.10)

We recognized, that among seventeen solutions presented by Chun in his paper twelve solutions (25), (27), (28) (30), (49), (51) (53), (55), (57), (69), (70) and (71) satisfy the fifth-order KdV equation, but solutions (25), (30), (69), (70) and (71) are trivial ones (constants) and (51) is not the solitary wave solution. Six solutions (25), (27), (49), (53), (55) and (57) are solitary wave solutions, but these ones are known and can be found by means of other methods.

Example 5e. Solutions of the improved Boussinesq equation by Abdou and co -authors  [65].

Using the Exp - function method Abdou and his co - authors looked for the solitary wave solutions of the improved Bouusinesq equation
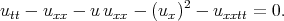utt - uxx - u uxx - (ux)2 - uxxtt = 0.
(6.11)

In the travelling wave Eq.(6.13) takes the form
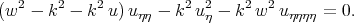(w2 - k2 - k2u) uηη - k2u2 - k2 w2 uηηηη = 0. η
(6.12)

The authors found several solutions of Eq.(6.12). One of them takes the form
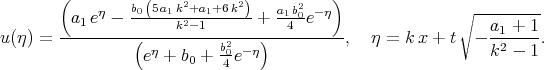( ) η b0(5a1k2+a1+6-k2)- a1b20 -η ∘ --------- a1 e - k2- 1 + 4 e a1 + 1 u(η) = ---------(--η-------b20--η)----------, η = k x + t - k2---1. e + b0 + 4 e
(6.13)

However this solution can be presented as
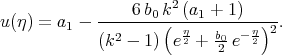-----6b0k2-(a1 +-1-)--- u(η) = a1 - 2 ( η2 b0 - η2)2. (k - 1) e + 2 e
(6.14)

Solution (6.14) can be obtained by many methods.

We have often observed the fifth error studying the application of the Exp - function method.

Other examples of the fifth error are given in our recent papers  [42, 46].

The EqWorld website presents extensive information on solutions to various classes of ordinary differential equations, partial differential equations, integral equations, functional equations, and other mathematical equations.

Copyright © 2004-2017 Andrei D. Polyanin