EqWorld logo

EqWorld

The World of Mathematical Equations

 IPM Logo

Exact Solutions Methods Software For Authors Math Forums

Exact Solutions > Interesting Papers > N.A. Kudryashov. Seven common errors in finding exact solutions of nonlinear differential equations > 8. Seventh error...

Seven common errors in finding exact solutions of nonlinear differential equations
© N.A. Kudryashov
Communications in Nonlinear Science and Numerical Simulation (to be pubslished in 2009)

Contents

  1. Abstract
  2. Introduction
  3. First error: some authors use equivalent methods to find exact solutions
  4. Second error: some authors do not use the known general solutions of ordinary differential equations
  5. Third error: some authors omit arbitrary constants after integration of equation
  6. Fourth error: using some functions in finding exact solutions some authors lose arbitrary constants
  7. Fifth error: some authors do not simplify the solutions of differential equations
  8. Sixth error: some authors do not check solutions of differential equations
  9. Seventh error: some authors include additional arbitrary constants into solutions
  10. Conclusion
  11. References

8. Seventh error: some authors include additional arbitrary constants into solutions

In finding the exact solutions of nonlinear differential equation our goal is to find the general solution. But it is not possible in many cases. In this situation we can try to look for the exact solutions with the larger amount of arbitrary constants. However we need to remember that the general solution of the equation of the n-th order can have only n arbitrary constants. Nevertheless we meet the papers, in which the authors present the solution of the Riccati equation with two or even three arbitrary constants. Moreover these authors say about the advantage of their approach in comparison with other methods taking into consideration the amount of arbitrary constants. Unfortunately in these cases there are two possible variants for this kind of solutions. The first variant is the author have obtained the solution with extra arbitrary constants and the amount of these constants can be decreased by means of the transformations. In the second variant the large amount of arbitrary constants in the solution points out that the author have found wrong solution.

So, we can formulate the seventh error as follows.

Seventh error. Some authors include additional arbitrary constants into solutions of nonlinear ordinary differential equations.

Example 7a. Solution of the Riccati equation
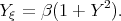Y = β(1 + Y 2). ξ
(8.1)

Using
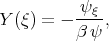Y(ξ) = - -ψξ-, β ψ
(8.2)

we obtain the linear equation of the second order
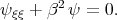2 ψ ξξ + β ψ = 0.
(8.3)

The solution of equation (8.1) takes the form
C3-e-iβξ---C4-eiβξ- Y (ξ ) = i C3 e-iβξ + C4 eiβ ξ.
(8.4)

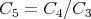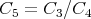At first glance we obtain more general solution (8.4) of the Riccati equation then (5.7), but in fact these solutions are the same. We can see, that one of the constants can be removed by dividing the nominator and the denominator in solution (8.4) on C3 (or on C4). Denoting C5 = C4 ∕C3 (or C5 = C3 ∕C4) we obtain the solution with the only arbitrary constant.

Example 7b. Solution of the Sharma - Tasso - Olver equation.

In example 2f we have obtained the solution of Eq.(3.36) in the form
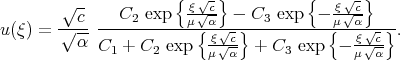{ √ -} { √-} √c- C2 exp ξμ√-cα- - C3 exp - μξ√cα- u(ξ) = √--- ------------{-ξ√c-}----------{--ξ√c-}. α C1 + C2 exp μ√α- + C3 exp - μ√-α-
(8.5)

However Eq.(3.36) has the second order, but solution (8.5) contains tree arbitrary constants. Sometimes it is convenient to leave three constants in solution (8.5), but we have to remember that solution (8.5) is not the general solution and one of these constants is extra. We can remove one of the constants as in example 7a and can write the general solution of Eq.(3.36) in the form
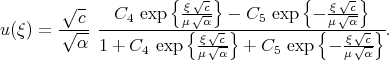{ √ -} { √-} √ - C4 exp ξ√-c- - C5 exp - -ξ√c- u (ξ ) = √-c- ----------μ{-α√--}----------{μ--α√-}-. α 1 + C4 exp ξμ√-cα- + C5 exp - μξ√cα-
(8.6)

Solution (8.6) of Eq.(3.36) is not worse then solution (8.5), but this solution is the general solution by definition and all other solution can be found from this one.

Example 7c. Solution (6.5) of the modified Benjamin - Bona - Mahony equation (6.3) [63]
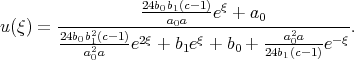24b0b1(c--1)eξ + a u (ξ) = ----2--------a0a---------0---2------. 24b0b12(c-1)e2ξ + b1eξ + b0 +--a0a--e-ξ a0a 24b1(c-1)
(8.7)

Solution (8.7) has three arbitrary constants a0, b0 and b1, but in fact this solution can be simplified to the form with one arbitrary constant as it was demonstrated in example 5c.

Example 7d. ”New exact solution” of the Riccati equation by Dai and Wang [76]
φ + l + φ2 = 0. ξ 0
(8.8)

Dai and Wang  [76] had been looking for the ”new exact solutions” of the Riccati equation (8.8) and obtained five solutions. One of them (solution (17) [76]) takes the form
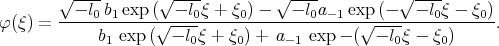√ ---- √ ---- √ ---- √ ---- ----l0-b1-exp-(√---l0ξ +-ξ0)-------l0a--1exp√-(-----l0ξ --ξ0)- φ (ξ) = b1 exp ( - l0ξ + ξ0) + a-1 exp - ( - l0ξ - ξ0) .
(8.9)

We can see, that solution (8.9) has three arbitrary constants, but two of them certainly can be removed.

Example 7e. Solutions of the Burgers - Huxley equation by Chun  [68].

Using the Exp - function method Chun  [68] obtained the generalized solitary wave solutions of the Burgers — Huxley equation (see, Eq.(8.10) in example 6e). One of his solution (solution (32) in  [68]) takes the form
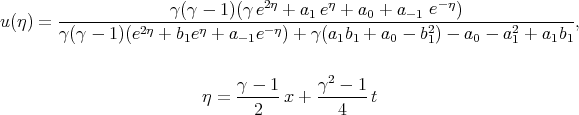--------------γ(γ---1)(γ-e2η-+-a1-eη +-a0-+-a--1 e--η)------------ u (η) = γ(γ - 1)(e2η + b1eη + a- 1e -η) + γ (a1b1 + a0 - b21) - a0 - a21 + a1b1, γ---1- γ2---1- η = 2 x + 4 t
(8.10)

The Burgers — Huxley equation is the second order one but solution (8.10) has three arbitrary constants. We suggested that this solution is incorrect. We checked this solution and have convinced that this solution does not satisfy Eq.(7.19).

Especially many solutions of equations with superfluous constants were obtained by means of the Exp - function method. Such examples can be found in many papers.

The EqWorld website presents extensive information on solutions to various classes of ordinary differential equations, partial differential equations, integral equations, functional equations, and other mathematical equations.

Copyright © 2004-2017 Andrei D. Polyanin