[1]     Zabusky N.J., Kruskal M.D. Ineraction of ”Solitons” in a collisioness plasma and the recurrence of initial states. Phys Rev Lett 1965; 15: 240-3

[2]     Gardner C.S., Green J.M., Kruskal M.D., and Miura R. M. Method for solving the Korteweg-de Vries equations. Phys Rev Lett 1967; 19: 1095 - 97

[3]     Lax P.D. Integrals of nonlinear equations of evolution and solitary waves. Communications on pure and applied mathematics 1968; 21: 467 - 90

[4]     Ablowitz M.J., Kaup D. J., Newell A. C., Segur H. The Inverse Scattering Transform - Fourier Analysis for Nonlinear Problems Stud. Appl Math 1974; 53: 249 - 315.

[5]     Ablowitz M.J. and Clarkson P.A. Solitons Nonlinear Evolution Equations and Inverse Scattering. Cambridge university press, 1991

[6]     Hirota R. Exact solution of the Korteweg-de Vries for multiple collinsions of solutions. Phys Rev Lett 1971; 27: 1192 - 94

[7]     Kudryashov N.A. Analitical theory of nonlinear differential equations. Moskow - Igevsk. Institute of computer investigations: 2004 [in Russian]

[8]     Polyanin A.D., Zaitsev V.F., Zhyrov A.I. Methods of nonlinear equations of mathematical physics and mechanics. Moscow. Fizmatlit: 2005

[9]     Weiss J., Tabor M., Carnevalle G. The Painleve property for partial differential equations. J Math Phys 1983; 24:522-26

[10]     Weiss J. The Painleve property for partial differential equations. II: Backlund transformation, Lax pairs, and the Schwarzian derivative. J Math Phys 1983; 24:1405-13

[11]     Conte R. The Painleve property, one century later, CRM series in mathematical physics, New York: Springer – Verlag; 1999. p. 77 - 180

[12]     Kudryashov N.A. Exact soliton solutions of the generalized evolution equation of wave dynamics. Journal of Applied Mathematics and Mechanics 1988; 52(3):360-5

[13]     Conte R., Musette M. Painlevé analysis and Backlund transformations in the Kuramoto - Sivashinsky equation. Journal of Physics A.: Math Gen 1989; 22:169-77

[14]     Kudryashov N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys Lett A 1990; 147:287-91

[15]     Kudryashov N.A. Exact soliton solutions of nonlinear wave equations arising in mechanics. Journal of Applied Mathematics and Mechanics 1990; 54(3):450-53

[16]     Kudryashov N.A., On types of nonlinear nonintegrable equations with exact solutions Phys Lett A 1991; 155:269-75

[17]     Kudryashov N.A. Partial differential equations with solutions having movable first - order singularities. Physics Letters A 1992; 169:237-42

[18]     Kudryashov N.A., Truncated expansions and nonlinear integrable partial differential equations. Physics Letters A 1993; 178:99-104

[19]     Kudryashov N.A. From singular manifold equations to integrable evolution equations. J Phys A Math Gen 1994; 27:2457-70

[20]     Kudryashov N.A., Zargaryan E.D., Solitary waves in active-dissipative dispersive media. J Phys A Math Gen 1996;29:8067-77

[21]     Peng Y.Z., Krishnan E.V. The singular manifold method and exact periodic wave solutions to a restricted BLP dispersive long wave system. Reports on mathematical physics 2005; 56:367 - 78

[22]     Kudryashov N.A., Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos, Solitons and Fractals 2005; 24:1217-31

[23]     Kudryashov N.A. Exact solitary waves of the Fisher equations. Physics Letters A 2005; 342:99-106

[24]     Kudryashov N.A., Demina M.V. Polygons of differential equation for finding exact solutions. Chaos Solitons and Fractals 2007; 33:1480-96

[25]     Kudryashov N.A. Solitary and Periodic Solutions of the Generalized Kuramoto -Sivashinsky Equation. Regular and Chaotic Dynamics 2008, 13:234-38

[26]     Kudryashov N.A., Loguinova N.B. Extended simplest equation method for nonlinear differential equations. Applied Mathematics and Computation 2008; 205:396-402

[27]     Lan H., Wang K. Exact solutions for some nonlinear equations. Physics Letters A 1989; 137: 369-73

[28]     Lou S.Y.,Huang G.X., Ruan H.Y. Exact solitary waves in a convecting fluid. J Phys A Math Gen 1991; 24(11):L587-L590

[29]     Malfliet W., Hereman W. The Tanh method: I Exact solutions of nonlinear evolution and wave equations. Phys Scripta 1996; 54:563-68

[30]     Parkes E.J., Duffy B.R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput Phys Commun 1996; 98:288-300

[31]     Wang M.L., Li X., Zhang J. The 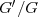- expansion method and evolution erquations in mathematical physics. Phys Lett A 2008; 372(4):417

[32]     Bekir A., Application of the 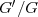- expansion method for nonlinear evolution equations. Phys Lett A 2008; 3400-06

[33]     Zhang J., Wei X., Lu Y. A generalized 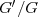- expansion method and its applicatioons, Phys. Lett. A 2008; 372:3653-58

[34]     Wazwaz A. M. The tanh - coth method for solitons and kink solutions for nonlinear parabolic equations. Appl Math Comput 2007; 188:1467-75

[35]     Abdou M. A. The extended tanh method and its applications for solving nonlinear physical models. Appl Math Comput 2007; 199:988-96

[36]     Wazzan L. A modified tanh - coth method for solving the general Burgers - Fisher and the Kuramoto - Sivashinsky equations. Commun Nonlinear Sci Numer Simulat, (2008), doi: 10.1016/j.cnsns.2008.08.004.

[37]     He J.H., Wu X.H. Exp-function method for nonlinear wave equations, Chaos Solitons Fractals 2006; 30:700 - 08

[38]     He J.H., Abdou M.A. New periodic solutions for nonlinear evolution equations using Exp-function method. Chaos, Solitons and Fractals 2007; 34:1421 - 29

[39]     Wu X.H., He J.H. Solitary solutions, peridic solutions and compaction - like solutions using the Exp-function method. Comput Math Appl 2007; 54:966 - 86

[40]     Ebaid A. Exact solitary wave solutions for some nonlinear evolution equations via Exp-function method. Phys Lett A 2007; 365:213 - 19

[41]     El - wakil S.A., Madkour M.A., Abdou M.A. Application of the Exp-function method for nonlinear evolution equations with variable coefficients. Phys Lett A 2007; 369:62 - 9

[42]     Kudryashov N.A., Loguinova N.B. Be carefull with the Exp - function method. Commun Nonlinear Sci Numer Simulat 2009; 14:1881 - 90

[43]    Li W., Zhang H. Generalized multiple Riccati equations rational expansion method with symbolic computation to construct exact complexiton solutions of nonlinear partial differential equations. Appl Math Comput 2008; 197: 288 - 96

[44]     Zhang S. Application of the Exp - function method to high - dimensional nonlinear evolution equation. Chaos, Solitons and Fractals 2008; 38:270 - 76

[45]     Korteweg D.J., de Vries G. On the change of form of long waves advancing in a rectangular canal and on a new tipe of long stationary waves. Phil Mag 1895; 39:422-43

[46]     Kudryashov N.A. , On ”new travelave solutions” of the KdV and the KdV - Burgers equations. Commun Nonlinear Sci Numer Simulat 2009; 14:1891-1900

[47]     Khani F. Analytic study on the higher order Ito equations: New solitary wave solutions using the Exp - function method. Chaos, Solitons and Fractals 2008; doi: 10.1016/j.chaos.2008.08.023

[48]     Öziş T., Aslan I., Exact and explicit solutions to the (3+1) - dimensional Jimbo - Miva equation via the Exp - function method. Phys Lett A 2008; 372:7011 - 15

[49]     Ganji Z.Z., Ganji D.D., Bararnia H. Approximate general and explicit solutions of nonlinear BBMB equations by Exp - function method. Applied Mathematical Modeling, 2008; doi: 10.1016/j.apm.2008.03.005

[50]     Erbas B., Yusufoǧlu E., Exp - function method for constructing exact solutions of Sharma - Tasso - Olver equation. Chaos, Solitons and Fractals 2008; doi: 10.1016/j.chaos.2008.09.003

[51]     Soliman A.A., Exact solutions of the KdV - Burgers equation by Exp-function method. Chaos, Solitons and Fractals, 2008; doi: 10.1016/J.chaos. 2008.04.038

[52]     Cole J.D. On a quasilinear parabolic equation occurring in aerodynamics. Quart Appl Math 1951 9:225 - 36

[53]     Hopf E. The partial differential equation 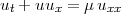. Commun Pure AppL Math 1950; 13: 201 - 30

[54]     Abdou M.A. Generalized solitonary and periodic solutions for nonlinear partial differential equations by the Exp - function method. Nonlinear Dynamics 2008: 52: 1-9, doi 10.1007/s1071-007-9250-1

[55]     Wazwaz A.M. Multiple - soliton solutions for the generalized (1+1) - dimensional and the generalized (2+1) - dimensional Ito equations. Applied Mathematics and Computation 2008; 202: 840 - 49

[56]     Clarkson P.A., Kruskal M.D. New similarity reductions of the Boussinesq equation. J Math Phys 1989; 30:2201 - 13

[57]     Ugurlu Y., Kaya D. Solutions of the Cahn - Hillard equation. Computers and Mathematics with Applications 2008; doi:10.1016/j.camwa.2008.07.007

[58]     Bekir A. On travelling wave solutions to combined KdV - mKdV and modified Burgers - KdV equation, Commun Nonlinear Sci Numer Simulat 2009 14:1038 - 42

[59]     Bekir A., Applications of the extended tanh method for coupled nonlinear evolution equations. Commun Nonlinear Sci Numer Simulat 2008; 13:1748 - 57

[60]     Xie F., Zhang Y., Lü Z. Symbolic computation in nonlinear evolution equation: application to (3+1) - dimensional Kadomttsev - Petviasvili equation. Chaos, Solitons and Fractals 2005; 24: 257 - 63

[61]     Zhang S.Symbolic computation and new families of exact non-travelling wave solutions of (2+1) - dimensional Konopelchenko - Dubrovsky equations. Chaos, Solitons and fractals 2007; 31:951 - 59

[62]     Wazwaz A.M. New solitons and kinks solutions to the Sharma - Tasso - Olver equation. Applied Mathematics and Computation 2007; 188:1205 - 13

[63]     Yusufoǧlu E. New solitary solutions for the MBBM equations using Exp-function method. Physics Letters A 2008; 372:442 - 46

[64]     Chun C., Soliton and periodic solutions for the fifth-order KDV equation with the Exp - function method, Physics Letters A 2008; 372: 2760 - 66

[65]     Abdou M.A., Soliman A.A., El-Basony S.T., New application of Exp - function method for improved Boussinesq equation. Physics Letters A 2007; 369:469 - 75

[66]     Bekir A., Cevikel A.C. Solitary wave solutions of two nonlinear physical models by tanh - coth method. Commun Nonlinear Sci Numer Simulat 2009; 14: 1804 - 09

[67]     Öziş T., Köroǧlu C., A novel approach for solving the Fisher equation using Exp-function method. Physics Letters A 2008; 372: 3836 - 3840

[68]     Chun C. Application of Exp-function method to the generalized Burgers - Huxley equation. Journal of Physics: Conference Series 2008; 96:012217

[69]     Efimova O.Yu., Kudryashov N.A. Exact solutions of the Burgers - Huxley equation. Journal of Applied Mathematics and Mechanics 2004; 68(3):413 - 20

[70]     El - Wakil S.A., Abdou M.A., Hendi A. New periodic wave solutions via Exp-function method. Phys Lett A 2008; 372:830 - 40

[71]     Zhang S. Exp-function method for Klein-Gordon equation with quadratic nonlinearity. J. Phys: Conference Series 2008; 96: 012002

[72]     Noor M.A., Mohyud-Din S.T., Waheed A., Exp-function method for solving Kuramoto—Sivashinsky and Boussinesq equations. J Appl Math Comput 2008; doi: 10.1007/s12190-008-0083-y.

[73]     Kuramoto Y., Tsuzuki T. Persistent Propagation of concentration waves in Dissipative media far from thermal equalibrium. Progress of theoretical Physics 1976; 55(2):356 - 69

[74]     Wazwaz A.M. New solitary wave solutions to the Kuramoto—Sivashinsky and the Kawahara equations. Applied Mathematics and Computation 2006; 182:164250.

[75]     Chen H., Zhang H. New multiple soliton solutions to the general Burgers-Fisher equation and the Kuramoto - Sivashinsky equation. Chaos, Solitons and Fractals 2004; 19:71 6.

[76]     Dai C.Q., Wang Y.Y. New exact solutions of the (3+1) - dimensional Burgers system. Physics Letters A 2008; doi:10.1016/j.physleta.2008.11.018