EqWorld logo

EqWorld

The World of Mathematical Equations

 IPM Logo

Exact Solutions Methods Software For Authors Math Forums

Exact Solutions > Interesting Papers > N.A. Kudryashov. Seven common errors in finding exact solutions of nonlinear differential equations > 7. Sixth error...

Seven common errors in finding exact solutions of nonlinear differential equations
© N.A. Kudryashov
Communications in Nonlinear Science and Numerical Simulation (to be pubslished in 2009)

Contents

  1. Abstract
  2. Introduction
  3. First error: some authors use equivalent methods to find exact solutions
  4. Second error: some authors do not use the known general solutions of ordinary differential equations
  5. Third error: some authors omit arbitrary constants after integration of equation
  6. Fourth error: using some functions in finding exact solutions some authors lose arbitrary constants
  7. Fifth error: some authors do not simplify the solutions of differential equations
  8. Sixth error: some authors do not check solutions of differential equations
  9. Seventh error: some authors include additional arbitrary constants into solutions
  10. Conclusion
  11. References

7. Sixth error: some authors do not check solutions of differential equations

Using the computer methods to look for the exact solutions of nonlinear differential equation we cannot remove our knowledge, our understanding and our attention to the theory of differential equations. Neglecting to do this we can obtain different mistakes in finding the exact solutions of nonlinear differential equations.

These mistakes lead to numerous misprints in the final expressions of the solutions and sometimes to the fatal errors. A need of verifying the obtained solutions is obvious and it does not take much time with the help of the modern computer algebra systems. We have to substitute the found solution into the equation and to check that the solution satisfies it.

The sixth error is formulated as follows.

Sixth error. Some authors do not check the obtained solutions of nonlinear differential equations.

Example 6a. ”Solutions” of the Burgers equation by Soliman  [51].

Soliman  [51] found three ”solutions” of the Burgers equation (4.1)
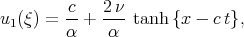c- 2-ν u1(ξ) = α + α tanh {x - ct},
(7.1)

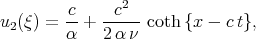2 u2 (ξ) = c-+ --c-- coth {x - ct}, α 2 α ν
(7.2)

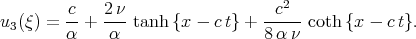c 2 ν c2 u3 (ξ ) = α-+ -α- tanh {x - ct} + 8-α-ν coth {x - ct}.
(7.3)

However all these solutions are incorrect and do not satisfy Eq.(4.1). The solution of Eq.(4.1) can be found by many methods and can be presented in the form
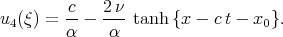c- 2ν- u4(ξ) = α - α tanh {x - ct - x0 }.
(7.4)

where x0 is arbitrary constant.

Example 6b. Solution of the foam drainage equation by Bekir and Cevikel  [66]
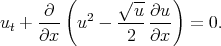( √ -- ) u + ∂-- u2 - --u-∂u- = 0. t ∂x 2 ∂x
(7.5)

Eq.(7.5) was studied in  [66] by means of the tanh - coth method by Bekir and Cevikel  [66]. The authors proposed the method to obtain ”new travelling wave solutions”.

Using the travelling wave
u(x, t) = u(ξ), ξ = k (x + c t),
(7.6)

they obtained the first - order equation in the form
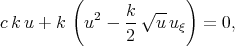( ) k√ -- ck u + k u2 - -- u uξ = 0, 2
(7.7)

and obtained three solutions
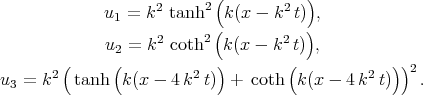( ) u = k2 tanh2 k(x - k2 t) , 1 ( ) u2 = k2 coth2 k(x - k2 t) , ( ( ) ( ))2 u3 = k2 tanh k (x - 4k2 t) + coth k (x - 4 k2 t) .
(7.8)

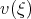The solution of Eq.(7.7) can be found using the transformation u = v2. For function v(ξ) we obtain the Riccati equation in the form
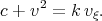c + v2 = k v. ξ
(7.9)

Solution of Eq.(7.9) can be written as
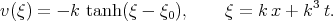3 v(ξ) = - k tanh (ξ - ξ0), ξ = k x + k t.
(7.10)

We can see there are the misprints in solutions of Eq.(7.7)

Example 6c. ”Solutions” of the Fisher equation by Öziş and Köroǧlu  [67]
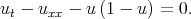ut - uxx - u (1 - u) = 0.
(7.11)

Using the Exp-function method Öziş and Köroǧlu  [67] found four ”solutions” of Eq. (7.11). These ”solutions” were given in the form
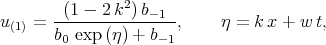(1 - 2k2 )b-1 u (1) = ---------------, η = k x + w t, b0 exp(η) + b-1
(7.12)

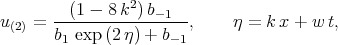2 u(2) = --(1---8k--)b-1--, η = kx + w t, b1 exp (2η) + b-1
(7.13)

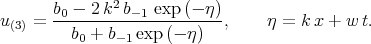b0 --2k2-b-1-exp(--η)- u (3) = b0 + b-1exp (- η) , η = k x + w t.
(7.14)

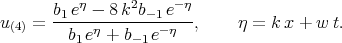b eη - 8k2b e-η u(4) = -1---η-------1--η--, η = k x + w t. b1e + b-1e
(7.15)

However all these expressions do not satisfy equation (7.11). We can note this fact without substituting solutions (7.12) - (7.15) into Eq. (7.11), because a true solution of Eq. (7.11) has the pole of the second order, but all functions (7.12) - (7.15) are the first order poles and certainly by substituting expressions (7.12) - (7.15) into equation (7.11) we do not obtain zero.

Example 6d. ”Solutions” of the modified Benjamin - Bona - Mahony equation (6.3) found by Yusufoglu  [63].

The general solution of Eq.(6.4) can be found via the Jacobi elliptic function, but the author tried to obtain some solitary solutions by means of the Exp - function method using the travelling wave 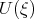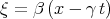U (ξ), ξ = β (x - γ t). Some of his solutions are incorrect. For example the ”solution” (formula (3.12) [63])
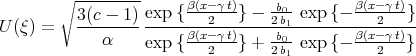∘ --------- β(x- γt) β(x-γt) 3(c - 1) exp {---2--} - 2b0b1 exp {- ---2--} U (ξ) = ---α---- -----β(x--γt)-----b0--------β(x--γt)- exp { 2 } + 2 b1 exp {- 2 }
(7.16)

do not satisfy Eq.(6.4).

The solution of Eq.(6.4) takes the form
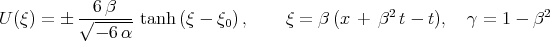--6β--- 2 2 U (ξ) = ± √ - 6α tanh (ξ - ξ0), ξ = β (x + β t - t), γ = 1 - β
(7.17)

This solution can be obtained by using different methods.

Example 6e. ”Solutions” of the Burgers - Huxley equation by Chun  [68].

Chun  [68] applied the Exp - function method to obtain the generalized solitary wave solutions of the Burgers — Huxley equation
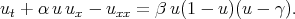ut + α uux - uxx = β u (1 - u )(u - γ ).
(7.18)

In the travelling wave the author looked for the solution of equation
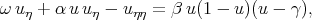ω uη + α uu η - u ηη = β u (1 - u )(u - γ ),
(7.19)

where 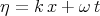η = kx + ω t. Some of the solutions by Chun are incorrect. In particular, ”solution” (25) in  [68]
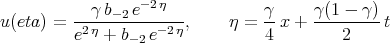-2η u(eta) = ---γ b-2-e----, η = γ-x + γ-(1 --γ-)t e2 η + b-2 e-2η 4 2
(7.20)

do not satisfy Eq.(7.19). The solutions of Eq.(7.18) were found in  [69].

Example 6f. ”Solutions” of the Benjamin - Bona - Mahony - Burgers equation by El-Wakil, Abdou and Hendi  [70].

El-Wakil and co-authors  [70] using the Exp - function method looked for the solitary wave solutions of the BBMB equation
ut - uxxt - αuxx + u ux + β ux = 0.
(7.21)

Taking the travelling wave 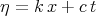η = kx + c t the authors searched for the solution of the equation
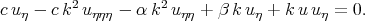cuη - ck2 uηηη - αk2 uηη + β ku η + k u uη = 0.
(7.22)

Some of solutions by El-Wakil and co-authors are incorrect. In particular, expression (18) in  [70]
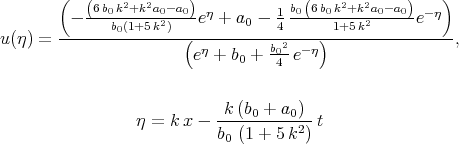( ) - (6b0-k2+k2a0-a0)eη + a - 1b0(6b0k2+k2a0-a0)e-η -------b0(1+5k2)-(-------0---4----)-1+5-k2---------- u(η) = eη + b + b02-e-η , 0 4 k (b + a ) η = k x - -----0---02- t b0 (1 + 5k )
(7.23)

do not satisfy Eq.(7.22).

The solutions of Eq.(7.22) can be found taking the different methods into account. Note that integrating Eq.(7.22) with respect to 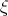ξ we have
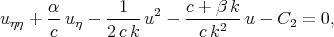α 1 c + β k uηη + --uη - -----u2 - ----2--u - C2 = 0, c 2 ck ck
(7.24)

where C2 is an arbitrary constant. Eq.(7.24) coincides with the KdV - Burgers equation in the travelling wave. The solitary wave solutions of this equation are given above in section 1. The general solution of Eq.(7.24) can be found by analogue with the general solution of Eq.(2.7)  [46].

Example 6g. ”Solutions” of the Klein — Gordon equation with quadratic nonlinearity by Zhang  [71].

The Exp - function method was used by Zhang to obtain the generalized solitonary solutions of the Klein - Gordon equation with the quadratic nonlinearity
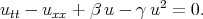2 utt - uxx + β u - γ u = 0.
(7.25)

The author  [71] applied the travelling wave 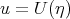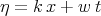u = U (η) η = k x + w t and searched for the solution of the equation
2 2 2 2 (w - k α )U ηη + β U - γ U = 0.
(7.26)

At least two solutions of Eq.(7.26) by Zhang  [71] are incorrect and do not satisfy Eq.(7.26)
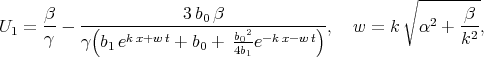∘ -------- U1 = β-- -(----------3-b0β---2--------), w = k α2 + -β-, γ γ b1ekx+w t + b0 + b04be- kx-wt k2 1
(7.27)

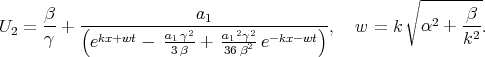∘ -------- β- ---------------a1-------------- 2 -β- U2 = γ + (ekx+wt - a1γ2+ a12γ2e-kx-wt) , w = k α + k2 . 3β 36β2
(7.28)

The solitary wave solutions of Eq.(7.26) was obtained in many papers, because this equation coincides with KdV equation in the travelling wave  [46]. These solutions can be written as the following
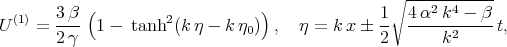∘ ------------ (1) 3-β ( 2 ) 1- 4-α2k4---β- U = 2 γ 1 - tanh (kη - k η0) , η = kx ± 2 k2 t,
(7.29)

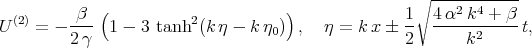∘----------- (2) -β- ( 2 ) 1- 4α2-k4-+-β- U = - 2 γ 1 - 3 tanh (k η - kη0) , η = k x ± 2 k2 t,
(7.30)

where 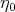η0 is an arbitrary constant.

Example 6h. ”Solutions” of the Kuramoto - Sivashinsky equation by Noor, Mohyud - Din and Waheed  [72].

Using the Exp - function method Noor, Mohyud-Din and Waheed  [72] looked for the solutions of the Kuramoto—Sivashinsky equation
ut + uux + uxx + uxxxx = 0.
(7.31)

These authors presented two expressions as the solutions of the Kuramoto - Sivashinsky equation. Their first ”solution” is written as
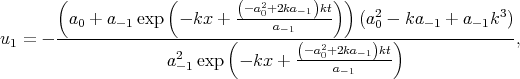( ( )) a + a exp - kx + (-a20+2ka-1)kt (a2- ka + a k3) ---0-----1-----------------a-1----------0------1-----1---- u1 = - 2 ( (-a20+2ka-1)kt) , a-1 exp - kx + a-1
(7.32)

where a0, 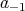a-1, k are arbitrary constants (formula (26) in  [72]).

The second ”solution” by the authors takes the form
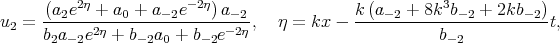2η -2η 3 (a2e--+--a0 +-a-2e---)a--2 k-(a--2 +-8k-b-2 +-2kb-2)- u2 = b2a-2e2η + b-2a0 + b-2e-2η, η = kx - b- 2 t,
(7.33)

where a0, a-2, a2, b0, b2, 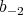b-2, k are arbitrary constants (formula (34) in  [72]).

Here we have the sixth common error in the fatal form. Substituting cited ”solutions” (7.32) and (7.33) into (7.31), we obtain that these ”solutions” do not satisfy the Kuramoto - Sivashinsky equation. Moreover, we cannot obtain zero with any nontrivial values of the parameters. We guess, that using the Exp - function method the authors  [72] did not solve the system of the algebraic equations for the parameters.

The exact solutions of Eq.(7.31) were first found in  [73]. These two solutions take the form
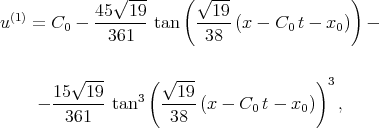√ --- ( √ --- ) (1) 45--19- --19- u = C0 - 361 tan 38 (x - C0 t - x0) - √ --- (√ --- )3 - 15--19-tan3 --19-(x - C0 t - x0 ) , 361 38
(7.34)

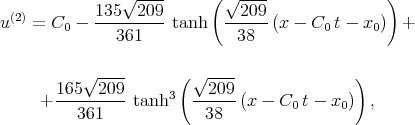√ ---- ( √ ---- ) (2) 135--209- --209- u = C0 - 361 tanh 38 (x - C0 t - x0) + √ ---- √ ---- 165 209 ( 209 ) + ---------tanh3 ------(x - C0 t - x0) , 361 38
(7.35)

where C0 and x0 are arbitrary constants.

Many authors tried to find new exact solutions of the Kuramoto - Sivashinsky equation (7.31). Some of authors  [36, 74, 75] believe that they found new solutions but it is not this case. Nobody cannot find new exact solutions of Eq.(7.31).

The EqWorld website presents extensive information on solutions to various classes of ordinary differential equations, partial differential equations, integral equations, functional equations, and other mathematical equations.

Copyright © 2004-2017 Andrei D. Polyanin